Presented at the Third International Conference on Creationism
Pittsburgh, PA, July 18-23, 1994
Copyright 1994 by Creation Science Fellowship, Inc.
Pittsburgh, PA  USA - All Rights Reserved

Genesis Flood, ocean currents, sediment transport, sedimentation patterns, shallow water equations

This paper presents results from a set of numerical experiments that explore the patterns of ocean circulation that arise when the earth's continental surface is mostly flooded. The calculations employ a code that solves the 2-D shallow water equations on a rotating sphere with surface topography. Several continental configurations are considered, including that of a single Pangean-like supercontinent. A surprising yet persistent feature in these calculations is the appearance of high velocity currents generated and sustained by the earth's rotation above the flooded continents. Water velocities in the deeper ocean by contrast are much smaller in magnitude. The patterns typically include strong cyclonic gyres at high latitudes with water velocities on the order of 40-80 m/s. The gyres tend to be compressed against the western continental margins and produce strong equatorward currents parallel to the western coastlines. The calculations argue that strong currents spontaneously arise over flooded continents. They suggest that accurate observational data on the current directions in the Paleozoic and Mesozoic rocks coupled with careful numerical modeling could be extremely fruitful in understanding the origin of much of the earth's sedimentary record.

A central question in understanding the Flood catastrophe is what was the hydraulic mechanism that was able to transport millions of cubic kilometers of sediment, to distribute most of it in widely dispersed layers--in many cases hundreds to thousands of kilometers in horizontal extent, and to accomplish such a vast amount of geological work in only a few months time. Clark and Voss [1] have suggested that resonant lunar tides might qualify as the primary mechanism. Such tides, if they were to occur with sufficient amplitude in the presence of the continents, could indeed erode and transport huge volumes of sediment and deposit the sediment in laterally extensive layers. A major difficulty with this idea is that the resonance condition for a smooth earth without continents is a water depth of about 8000 m [1,4]. This represents about three times the volume of water currently in the world's oceans. Resonance, however, can occur at higher spatial harmonics and smaller water depths. For a smooth earth the critical water depth for the next higher harmonic is about 2000 m [1,4], much closer to the amount of water currently at the earth's surface. But the strength of the resonance of this mode is much smaller than that of the fundamental mode. It is not clear if the effects of bottom friction and other sources of dissipation are small enough for a resonant tide in this higher mode to arise even on a smooth earth, much less for an earth with realistic topography. Detailed numerical calculations are still needed to resolve these uncertainties.

In the process of exploring the possibility of a more localized tidal resonance in the large bay on the eastern side of the Pangean supercontinent known as the Tethys Sea, an entirely different mechanism was identified. It was found that the Coriolis force arising from the earth's rotation produces strong currents on top of the flooded continents independent of any tidal forcing. These currents form closed paths that generally have the same sense of rotation as the jet streams in the atmosphere, that is, cyclonic, or counterclockwise in the northern hemisphere and clockwise in the southern hemisphere. They are stronger above a continent localized to higher latitudes where the Coriolis force is stronger that for the same continent at lower latitudes. For continental flooding depths up to several hundred meters, these currents typically achieve speeds of several tens of meters per second, which is sufficiently strong to reduce the water depth to zero in much of the region enclosed by the cyclonic patterns of flow. Such speeds are easily adequate to erode by cavitation processes [3] and transport huge volume of relatively coarse clastic sediment for large distances.

This paper describes a set of numerical experiments using a code that solves the shallow water equations on the sphere to explore the necessary conditions and dynamical characteristics of these currents. This work is seen as only a beginning effort to understand this phenomenon. It should be emphasized here that tidal effects in general would add to rather than compete with the flow produced by such currents. These Coriolis force driven currents then are almost certainly only one of several factors responsible for the large scale sedimentation patterns during the Flood.

The shallow water equations describe the behavior of a shallow homogeneous incompressible and invicid fluid layer. On a rotating sphere these equations may be expressed [8, p. 213]

	du/dt=- f k x u - g h	(1)
and
	dh*/dt=- h* u,	(2)

where u is horizontal velocity (on the sphere), f is the Coriolis parameter (equal to 2W sin q for rotation rate W and latitude q), k is the outward radial unit vector, g is gravitational acceleration, h is the height of the free surface above some spherical reference surface, and h* is the depth of the fluid. If h_t denotes topography on the sphere, then h=h* + h_t. The d/dt operator is the material or substantial or co-moving time rate of change of an individual parcel of fluid. The 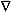operator is the spherical horizontal gradient operator and the 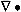operator is the spherical horizontal divergence operator. These simple equations are appropriate when the depth of the fluid is small compared with the important horizontal length scales. This criterion is satisfied for the problem at hand where the water depths are typically less than four kilometers while the horizontal dimensions of ocean basins and continents are measured in thousands of kilometers. Also note that the fluid density does not appear in these equations. This means that to the degree the approximations apply, the same equations describe flow in both the atmosphere and oceans.

These equations are solved in discrete fashion on a mesh constructed from the regular icosahedron as shown in Fig. 1. The mesh has 40962 nodes and the spacing between nodes is about 125 km. A separate spherical coordinate system is defined at each node such that the equator of the system passes through the node and the local longitude and latitude axes are aligned with the global east and north directions. This approach has the advantage that the coordinates are almost Cartesian and only two (tangential) velocity components are needed. A semi-Lagrangian formulation [7] of equations (1) and (2) is used which involves computing the trajectories during the time step that end at each node. Values for h and u at the beginning of the time step at the starting point of each trajectory are found by interpolating from the known nodal values at the beginning of the time step. Changes in h and u along the trajectory are computed using (1) and (2). This Lagrangian-like method eliminates most of the numerical diffusion that is associated with Eulerian schemes. Second-order accurate interpolation is used to find the starting point values of the trajectories. This formulation using the icosahedral mesh has been carefully validated using the suite of test problems developed by Williamson et al. [8].

A small set of problems was investigated to explore some of the conditions under which a coherent pattern of strong currents arises on top of a flooded continent. Fig. 2 is a sequence of snapshots from a calculation initialized with a Pangean-like distribution of continent of uniform height flooded to a depth of 500 m. The ocean depth is also taken to be a uniform value of 3980 such that the total water volume equals that in the present oceans and ice caps. The initial velocity field is everywhere zero. Fig. 2 (a) displays the initial height of the water above the bottom topography. Frames (b)-(g) in Fig. 2 show the development of the pattern of flow with time at 10 day intervals. Two closed circulations, one in the northern hemisphere and one in the southern, emerge from the initial state. The sense of rotation of these circulations is cyclonic, which implies low pressure or reduced surface height inside the circulations. By a time of 30 days the currents are so strong that the water depth has decreased to zero over portions of the continental surface inside circulating flows. The current velocities continue to increase to peak values of about 87 m/s until the 50 day snapshot after which time there is no significant change in the peak velocity. The patterns show prominent wavelike structure in the latitude zone between 20? and 50?. In the atmosphere such features are known as planetary waves. They occur because of the variation of the Coriolis parameter with latitude and are also referred to as Rossby waves [5, p.93-95].

The effect of increasing the depth of flooding to a value of 1000 m is shown in Fig. 3. In this case the time dependence of the pattern is much stronger, the peak velocities are somewhat lower at about 78 m/s, and the reduction of the surface height inside the regions of cyclonic flow is approaching 1000 m. Snapshots at 80 and 90 days reveal how dramatically the flow pattern varies with time. Usually there is more than one cyclonic gyre in a given hemisphere. Fig. 4. shows the effect of increasing the depth of continental flooding further to 1500 m. Under these circumstances the peak velocities are reduced by almost a factor of two to about 40 m/s and the peak drawdown of the surface inside the cyclonic gyres is only about 500 m. The time variation of the pattern is still strong and the number of gyres is somewhat larger. Well-defined anticyclonic gyres are also evident. This latter case suggests that when the static water depth over the continent exceeds 1000 m, the strength of these currents begins to diminish significantly.

The calculations described thus far all used the same Pangean-like continent. To determine what role the special geometry of this continent might be playing in producing the observed patterns of flow, several cases were run with simpler continental geometries. Fig. 5 shows the results from a configuration consisting of a circular continent 50? (5560 km) in diameter centered at 45? latitude in each hemisphere. The depth of flooding is 1000 m. The snapshot at 80 days shows single cyclonic gyres on each continent with peak velocities of about 40 m/s and reductions in surface height of about 400 m. Moderate time dependence is present. When these continents are moved to points centered at 60? latitude, the character of the solution remains the same but the strength of the flow increases to yield peak velocities of about 55 m/s and a maximum reduction in the surface height of about 1000 m. On the other hand, when the circular continents are moved such that they are centered at 30? latitude, the peak velocity falls to about 37 m/s and the maximum reduction in surface height is only about 200 m. These results reflect the fact that the magnitude of the Coriolis parameter increases with the sine of the latitude. Calculations using circular continents are thus found to yield the same general behavior as observed for the Pangean-like continent.

Another issue that was addressed was the minimum horizontal dimension for a continental region required to obtain the strong gyre-like flow. Fig. 6 displays results for a configuration consisting of a circular continent 30? (3330 km) in diameter centered at 45? latitude in each hemisphere. The depth of flooding is 250 m. The snapshot at 40 days shows nicely developed gyres on each continent with a peak velocity of about 40 m/s. The identical case except for a continent diameter of 20? (2220 km), however, fails to produce any such feature. From these relatively small number of tests, it is inferred that there is a minimum critical dimension on the order of 2500 km below which this phenomenon does not occur.

The tendency for strong cyclonic gyres to form above flooded continents, particularly at the higher latitudes, appears to be a robust characteristic of the earth's ocean. Physically, these patterns of flow arise because of the earth's rotation and are influenced by the fact that the Coriolis parameter varies with latitude and that transport of absolute vorticity is a strongly nonlinear process. The absolute vorticity is defined as z + f, where z=curl u is the fluid vorticity in the shallow water limit and f is the Coriolis parameter. To good approximation the transport of absolute vorticity is described by the vorticity equation [5, p. 95]

d(z+ f)/dt=- (z+ f) u

(3)

For the situation of constant water depth, the velocity divergence 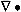u is zero. Equation (3) in this case requires a parcel of fluid moving equatorward have its vorticity z increase since f decreases with decreasing latitude, while the opposite holds for a poleward moving parcel. Thus there is transfer of vorticity from the earth's rotation to the fluid and vice versa. Because absolute vorticity itself depends on the local fluid velocity u through z, the right hand side of (3) is seen to be nonlinear in terms of velocity, and the dynamics associated with the vorticity therefore are highly nonlinear. Equation (3) can also be expressed as the conservation of potential vorticity, which is defined as (z+f)/h*, where h* is water depth [5, p. 96]. Since potential vorticity is inversely proportional to h*, the nonlinear dynamics are accentuated where the water is shallow. This suggests why high velocity currents arise in the shallower depths above the continents and not in the regions of deep ocean. For such strongly nonlinear problems, physical reasoning can only take one so far, and numerical simulation is generally the most practical means for obtaining deeper understanding of the system dynamics.

Calculations described above suggest there exists a minimum diameter for the strong gyres on the order of 2500 km. This seems to account for the absence of such features today since the present continental shelves are much narrower than this minimum scale length. On the other hand, the sedimentary record indicates there have been several major, apparently global, transgressions of the ocean over the continents since the beginning of the Cambrian period. In the case of North America, Sloss [6] has described six such major transgressions. The basal formation of the second transgression that occurred during the Ordovician is composed of extremely pure quartz sand and known as the St. Peter Sandstone [2, pp. 221-225]. It is readily identified and covered a large fraction of North America. The continental areas flooded by epeiric sea during such major transgressions easily exceed the 2500 km dimension. It is difficult then to imagine how strong currents such as observed in the numerical experiments did not arise and play a major role in development of the sedimentary record. Given the fact that catastrophic cavitation occurs for water velocities generally above 30 m/s [3], one would also expect severe and rapid erosion to be associated with any major transgression of the continents by the ocean. These phenomena relating to very fundamental aspects of sedimentary geology, to the authors' knowledge, have never before been considered or addressed in the scientific literature.

Numerical solution of the shallow water equations on a rotating sphere with parameters appropriate to the earth and flooded continental topography yields closed patterns of flow with velocities of 40 to 80 m/s and length scales typically 2500-5000 km above the flooded continental regions. Such currents would be expected to arise in the context of a global Flood as described in Scripture when "all the high mountains everywhere under the heavens were covered" with water (Gen. 7:19). The ability of such currents, combined with cavitation, to erode huge volumes of rock and also to transport the resulting sediment and distribute it over extensive areas in a short span of time not only helps to satisfy the Biblical time constraints for the Flood but also appears to be able, in a general sense, to account for the continent-scale extent of many Paleozoic and Mesozoic sedimentary formations as well as evidence in many of these rocks for high energy water transport. Clearly, calculations with more detailed and realistic topography that is allowed to change with time are the next step in this research program. If such calculations prove to be able to reproduce some of the primary features of the sedimentary record, then confidence that the Phanerozoic portion of geological history is indeed a consequence of Noah's Flood should spread substantially beyond its present bounds.