 Last month’s article explored initial problems with the isochron age model, which has been the standard radioisotope dating method.1 We will now dive even deeper into the isochron dating model. In part 1, we examined the linear equation in isotope ratios used as the basis for the model:
Last month’s article explored initial problems with the isochron age model, which has been the standard radioisotope dating method.1 We will now dive even deeper into the isochron dating model. In part 1, we examined the linear equation in isotope ratios used as the basis for the model:
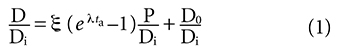
And the resulting age equation derived from it:
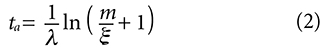
The Testable Assumptions
It was noted that time (age) is not directly measured in the isochron dating model but is a derived quantity and is essentially a third variable in the linear equation from which it is derived. The closed system assumption and the assumption that the model allows the accurate determination of the initial number of daughter nuclei when the rock solidified are both characteristic of all isotope pairs used in obtaining isochron model ages and were summarized in equations (2) thru (4) of Part 1. They are:
All daughter isotopes added to any sample result from decay of the parent isotope:

The number of parent isotopes decayed equals the original number of parent isotopes minus the present number of parent isotopes:

The number of daughter isotopes currently present in the sample is equal to the initial number plus the number added via decay of the parent:

Next is the homogeneous assumption that the initial daughter isotope and the index daughter isotope are uniformly distributed throughout the rock formation when the rock formation solidified. This then replaces the assumption that we can know the initial number of parent or daughter isotopes present in each rock sample:

It’s also assumed that enough parent isotope has decayed into the daughter isotope that it can actually be measured. After one billion years, this would be just 1.5% of the initial number of 87Rb parent nuclei. On the other hand, after 6,000 years it would only be approximately 0.0000085% of the initial number of 87Rb parent nuclei. This extremely small amount would not be detectable with current technology. So, assuming deep time is a critical assumption in age calculations using the isochron dating model.
The final basic assumption that the decay constant remains constant through all time and under all possible conditions has already been falsified2-5 due to contrary observable evidence.
What Do the Data Say?
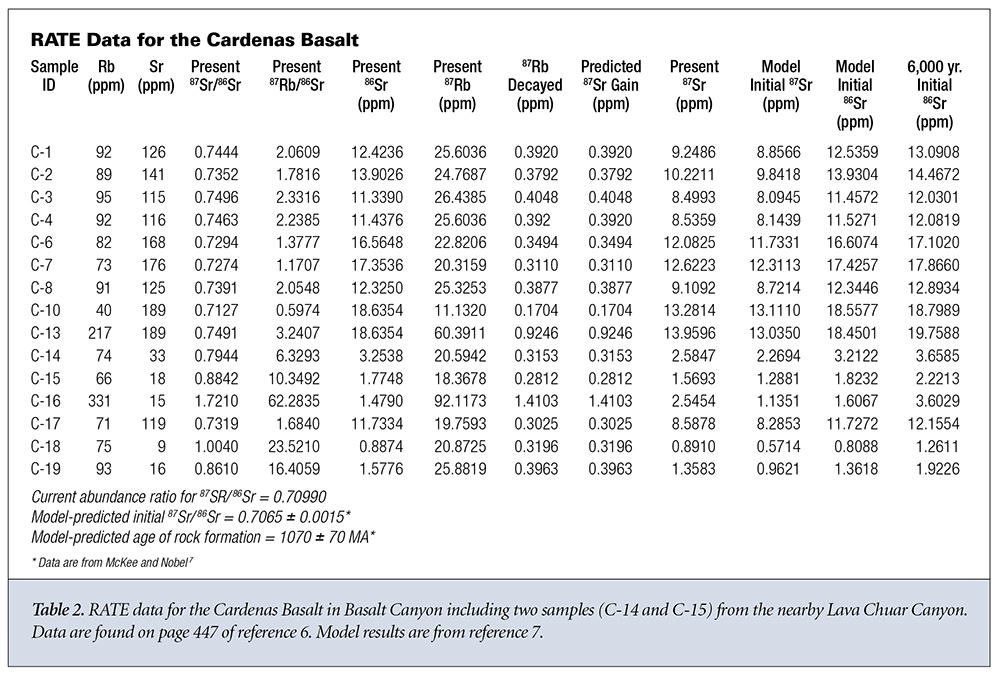
What do the data say about the first three assumptions? Let’s look at two sets of data from different rock strata in Grand Canyon. The first data group is from the Bass Rapids diabase sill6 and is displayed in Table 1. The second data group is from the Cardenas Basalt6 and is displayed in Table 2. Because no graphical data were given for the Cardenas Basalt, I used data from reference 7 for the isochron model predictions concerning the Cardenas Basalt.
Let’s start with the Bass Rapids data. For each sample, the measured values for natural Rb and natural Sr are given in columns 2 and 3. D and P are presented as measured values in columns 4 and 5. The current values of 86Sr and 87Rb in each sample are given in columns 6 and 7. These are obtained by multiplying the corresponding values in columns 2 and 3 by the currently known natural abundances of 87Rb and 86Sr. This assumes that the Rb and Sr distribute themselves through every sample according to currently known abundance ratios.
Using the standard radioactive decay equation, we can then back calculate the amount of 87Rb that should decay in 1.082 billion years; this is shown in column 8. According to the closed system assumption, the concentration of 87Sr should be equal to the concentration of 87Rb that has decayed, as calculated in column 9. Next, we calculate the actual amount of 87Sr present in the sample by multiplying the current 86Sr concentration (column 6) times the present 87Sr/86Sr ratio (column 4). This yields a value for the actual amount of 87Sr present in the sample. The value of 87Sr present varies from 4 to over 500 times the amount that could have been gained via simple radioactive decay. Finally, we calculate the initial amount of 87Sr, according to the model, when the rock system solidified by subtracting the projected amount of 87Sr added via decay (column 9) from the present amount of 87Sr in the sample (column 10).
From this initial amount of 87Sr (column 11) we can now estimate the original amount of 86Sr (column 12) in each sample by dividing the initial amount of 87Sr (column 11) by the model-predicted 87Sr/86Sr ratio at formation of the rock system. If we use a 6,000-year age for the rock formation, then the predicted 87Sr gain (column 9) is unmeasurable and can be set to zero. If we then divide the present amount of 87Sr (column 10) by the model-predicted 87Sr/86Sr ratio at formation of the rock system, we obtain slightly different predictions for the initial amount of 86Sr (column 13).
Let’s now apply the same analysis outlined above to the Cardenas Basalt.6,7 This time we find that the value of 87Sr gained by the sample varies from 3 to 78 times the amount that could have been gained via simple radioactive decay, except for sample C-16. Otherwise, the same general trends as observed for the Bass Rapids diabase sill samples are observed for the Cardenas Basalt samples.
Analysis
Within experimental and calculational errors, the final measured and projected initial amounts of 86Sr seem to remain the same within each sample. The Bass Rapids diabase sill samples are approximately equally divided between those that give values for the amount of initial 86Sr that are greater than the present amount of 86Sr and those that give greater amounts for the present 86Sr. Likewise for the Cardenas Basalt samples. Both groups display present 87Sr amounts greater than the initial 87Sr amounts. This is to be expected since this is the way the model was designed. It’s also interesting to note that if an age of 6,000 years rather than one billion-plus years is used, the projected initial amount of 86Sr is uniformly greater than the presently measured amount of 86Sr for each sample in both groups, evidence for movement of the 86Sr out of the samples.
The amount of 86Sr varies significantly from sample to sample, negating the assumption that it is uniformly distributed throughout the rock formation when it solidifies. The observed distribution is more likely due to differential isotopic diffusion and/or fractionation. Whatever the case, the original 87Sr/86Sr ratio has not reached a uniform value throughout the rock system during formation as is assumed in the isochron dating model. While the initial and final measured values of 86Sr and 87Sr are reasonably consistent within each sample, it’s clear that there’s a significant variation from sample to sample that’s inconsistent with the initial 87Sr/86Sr ratio being constant throughout the rock system. The 87Sr added to each sample cannot be explained by a simple linear replacement hypothesis. The decay of 87Rb adds a significantly smaller amount of 87Sr to each sample than already exists when the rock system was initially formed.
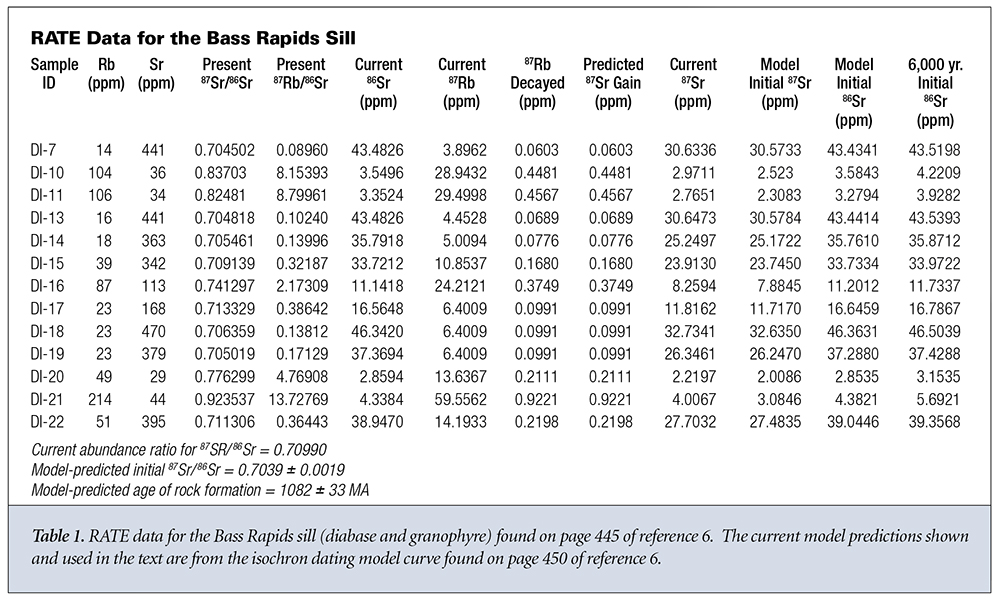
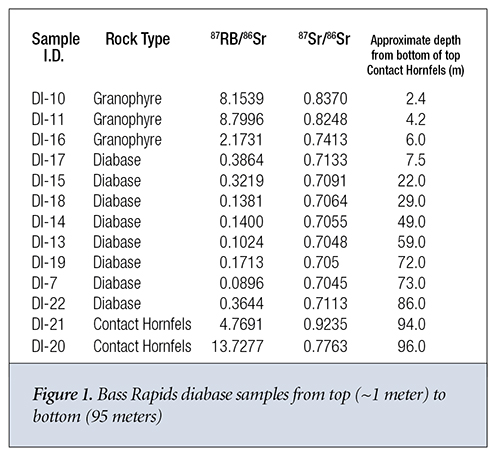 The 87Sr/86Sr ratio is approximately constant in the diabase from 30 meters to 75 meters (m) in depth measured from the top contact hornfels layer. It then steadily increases from 30 m to the top of the diabase column at around 7 m (Figure 1) where it interfaces with the capping granophyre. Near the interface with the bottom granophyre at around 85 m, the ratio returns to its value near the top of the diabase column. The Rb concentration also steadily increases from a depth of 60 m in the diabase to depth of 20 m from the top of the diabase where it experiences an ~40% decrease. Its value at the bottom of the diabase column where the diabase is in close contact with the contact hornfels is significantly higher than anywhere else in the diabase column. The 87Sr/86Sr ratios and Rb concentrations are significantly higher in both the granophyre and contact hornfels than they are in the diabase column, as pointed out by Dr. Andrew Snelling.6
The 87Sr/86Sr ratio is approximately constant in the diabase from 30 meters to 75 meters (m) in depth measured from the top contact hornfels layer. It then steadily increases from 30 m to the top of the diabase column at around 7 m (Figure 1) where it interfaces with the capping granophyre. Near the interface with the bottom granophyre at around 85 m, the ratio returns to its value near the top of the diabase column. The Rb concentration also steadily increases from a depth of 60 m in the diabase to depth of 20 m from the top of the diabase where it experiences an ~40% decrease. Its value at the bottom of the diabase column where the diabase is in close contact with the contact hornfels is significantly higher than anywhere else in the diabase column. The 87Sr/86Sr ratios and Rb concentrations are significantly higher in both the granophyre and contact hornfels than they are in the diabase column, as pointed out by Dr. Andrew Snelling.6
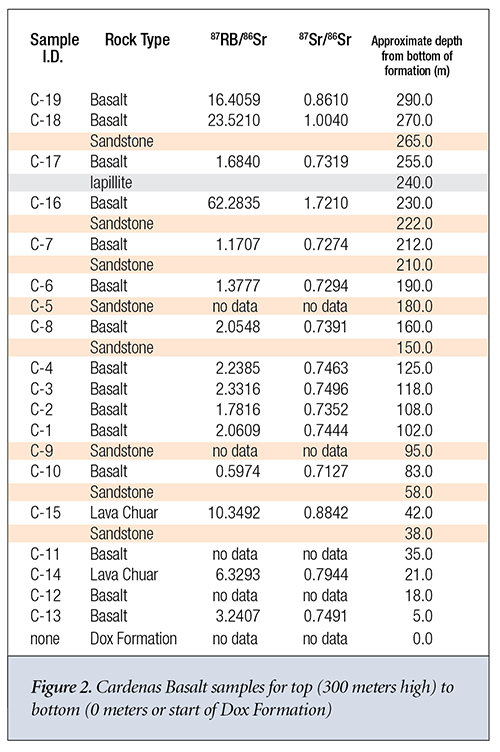
It’s much more difficult to discern any trends for the Cardenas Basalt. Samples C-6, C-8, C-4, C-3, C-2, and C-1 appear to exhibit some consistency in their Rb content and their 87Sr/86Sr isotope ratio. C-16 is the only sample where the isochron dating model-predicted 87Sr gain from 87Rb decay equaled or exceeded its predicted initial 87Sr in the sample at the time of formation. This was perhaps due to the proximity of sample C-16 to the Iapillite layer. Otherwise, they seem to exhibit the type of extreme variance one would expect from successive layers of basalt sandwiched by water-deposited sandstone. These samples appear consistent with a sequential global flood and substantial movement of isotopes via hydrothermal transport.
Conclusions
The observed amounts and ratios of 86Sr, 87Sr, and 87Rb are primarily determined by pre-existing amounts of said isotopes, as would be expected for the mixing of two or more different rock types solidifying as they mix together. This is supported by the data. The ratios obtained seem to have very little relationship with decay time (age) or decay rates. The closed system assumption, the homogeneity assumption, and the constant initial ratio of 87Sr/86Sr don’t appear to be supported by the data. These problematic issues combine to nullify the isochron model as a valid dating method.
Click here for Revisiting the Isochron Age Model, Part 1.
References
- Cupps, V. R. 2020. Revisiting the Isochron Age Model, Part 1. Acts & Facts. 49 (6): 10-13.
- Bosch, F. et al. 1996. Observation of Bound-State β − Decay of Fully Ionized 187Re: 187Re−187Os Cosmochronometry. Physical Review Letters. 77 (26): 5190-5193.
- Cardone, F., R. Mignani, and A. Petrucci. 2009. Piezonuclear decay of thorium. Physics Letters A. 373 (22): 1956-1958.
- Jenkins, J. H., D. W. Mundy, and E. Fischbach. 2010. Analysis of environmental influences in nuclear half-life measurements exhibiting time-dependent decay rates. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 620 (2-3): 332-342.
- Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. 2005. Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. El Cajon, CA: Institute for Creation Research.
- Snelling, A. A., Isochron Discordances and the Role of Inheritance and Mixing of Radioisotopes in the Mantle and Crust, Radioisotopes and the Age of the Earth, 393-524.
- McKee, E. H. and D. C. Nobel. 1976. Age of the Cardenas Lavas, Grand Canyon, Arizona. Geological Society of America Bulletin. 87 (8): 1188-1190.
* Dr. Cupps is Research Associate at the Institute for Creation Research and earned his Ph.D. in nuclear physics at Indiana University-Bloomington.













