Covering a flat surface with some pattern of geometric shapes with no overlaps or gaps is called tiling. Tiling shows up in many places, from the tiles on our kitchen floors to bees’ honeycombs. They generally have a pleasing, even fascinating, quality, and their regularity often expresses some natural harmony.
The most familiar kinds of tiling, such as covering a floor with squares that meet edge-to-edge, are examples of periodic tiling. In his 1619 Harmonice Mundi, Johannes Kepler created the first list of all the Archimedean tilings, those that can be created from sets of regular polygons. These kinds of tiling inherently possess many symmetries.
On the other hand, a Penrose tiling is an example of an aperiodic—irregular or not periodic—tiling. Tiling is aperiodic if it doesn’t contain arbitrarily large periodic regions or patches. Penrose tiling is named after the mathematician, physicist, and Nobel laureate Roger Penrose, who investigated it in the 1970s.1 Remarkably, Penrose tiling has an infinite number of different patterns that tile the entire plane, not just a single pattern in which every pattern one sees is a portion of the overall singular pattern.2 Thus, it almost resembles a disordered order.
Interestingly, if one counts the two shapes in the Penrose pattern (whether they are pentagons and rhombi, kites and darts, etc.) and divides the number of the larger shape (i.e., pentagons or kites) by the number of the smaller shapes (i.e., rhombi or darts), the result is 1.618. This is the golden ratio—a mathematical constant that’s found throughout nature, including in the proportions of the human body, the DNA structure, and the solar system.3,4
And the Penrose pattern gets more interesting if straight lines are drawn on the tiles. The lines are called Ammann bars after Robert Ammann, who further refined the matching rules necessary to properly lay out a Penrose pattern. When the pattern is put together, the tiles’ individual lines all connect perfectly into straight lines across the entire Penrose pattern (see the accompanying illustration).
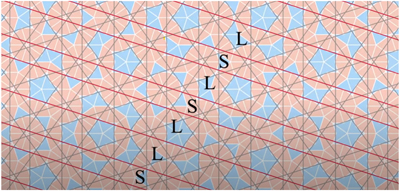
There are five sets of parallel lines, but they are not perfectly regular. There are two different spacings, long and short, that do not follow a periodic pattern. Counting the number of longs and shorts in any section allows one to derive the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, etc.)—a sequence in which each number is the sum of the two preceding numbers. This sequence is seen in mathematics, nature, computer science, and optics among other observations and uses. Furthermore, the ratio of one Fibonacci number to the previous one approaches the golden ratio.5
Even though this world is fallen and subject to futility (Genesis 3), evidence of design and order—even in an aperiodic, irrational pattern like a Penrose tiling—shines through. Discoveries like these provide compelling evidence that our world and its fundamental principles exhibit a remarkable degree of fine-tuning.6
In Colossians 1:16–17, the apostle Paul speaks of the Designer who’s the source of this exquisite order: “For by Him all things were created that are in heaven and that are on earth, visible and invisible, whether thrones or dominions or principalities or powers. All things were created through Him and for Him. And He is before all things, and in Him all things consist.”
References
- Grünbaum, B. and C. G. Shephard. 1987. Tilings and Patterns. New York: W. H. Freeman.
- Penrose, R. 1978. Pentaplexity. Eureka. 39: 16–22.
- Gardner, M. 1977. Mathematical Games: Extraordinary nonperiodic tiling that enriches the theory of tiles. Scientific American. 236 (1): 110–121.
- Livio, M. 2002. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway Books.
- Posamentier, A. and I. Lehmann. 2007. The Fabulous Fibonacci Numbers. New York: Prometheus Books.
- The Penrose pattern can be found in nature via quasicrystals originally discovered by Dr. Dan Shechtman in 1982. Since then, hundreds of quasicrystals have been reported and confirmed. Quasicrystals are currently being explored for applications ranging from non-stick electrical insulation and cookware to ultra-durable steel. See Glotzer, S. 2019. Quasicrystals: the thrill of the chase. Nature. 565: 156–158.
Stage image: Tiling in the Pilgrimage Church of Saint John of Nepomuk at Zelena Hora, Czech republic
Stage image credit: Copyright © Janswart, 2019. Used in accordance with federal copyright (fair use doctrine) law. Usage by ICR does not imply endorsement of copyright holder.
* Dr. Corrado earned a Ph.D. in Systems Engineering from Colorado State University and a Th.M. from Liberty University. He is a freelance contributor to ICR’s Creation Science Update, works in the nuclear industry, and is a senior officer in the U.S. Naval Reserve.










