Radioactive dating methods—many of which are quite elaborate—have numerous physical condition requirements that cannot realistically remain unaffected over millions and perhaps billions of years. Since the potassium-argon dating methods clearly appear to be unreliable, why should any rational person trust them to provide accurate dates for rocks?

In the early 1950s, scientists established theories for using the decay of radioactive potassium (⁴⁰K) to argon (⁴⁰Ar) as a clock for dating certain types of rocks. Called “noble” because it rarely bonds with other elements, argon (Ar) is one of the six noble gases. The others include helium (He), neon (Ne), krypton (Kr), xenon (Xe), and radon (Rn).

As one of the most abundant isotopes in the earth’s crust, K is an ideal candidate to use as a “rock clock.” Out of a wide array of available test methods, ⁴⁰K is one of those unusual radioisotopes that exhibit all three forms of beta decay:

• Electron decay
• Electron capture
• Positron decay

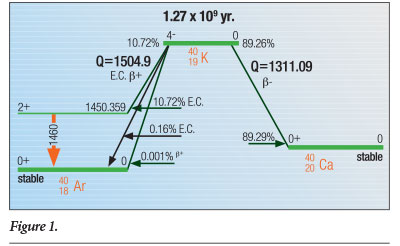Almost 90% of ⁴⁰K decays occur when one of its neutrons emit an electron (or beta particle) as it transmutes to the ground state—the state in which the nucleus is stable (not excited) and not decaying—of ⁴⁰Ca (calcium). The second-most prominent decay mode is through electron capture by one of its protons, which converts it to an excited state of the noble gas ⁴⁰Ar that then decays to the ⁴⁰Ar ground state by emitting a 1.4608 MeV gamma ray.¹ The electron capture decay mode can also proceed directly to the ground state of ⁴⁰Ar for 0.16% of ⁴⁰K decays. Finally, a positron decay mode to the ground state of ⁴⁰Ar has been observed in approximately 0.001% of ⁴⁰K decays. Figure 1 schematically illustrates these three processes.

Potassium (K), along with lithium (Li), sodium (Na), rubidium (Rb), and caesium (Cs), is an alkali metal that reacts violently with water, air, and the halogen elements (fluorine, chlorine, bromine, iodine, and astatine). It is so chemically reactive that it must be stored under oxygen-free liquid paraffin to prevent oxidation. Thus, it can move somewhat freely in most rock matrices. Most minerals that can incorporate calcium or sodium into their structure can also accommodate potassium, since all three elements have similar atomic radii. Interestingly, the ⁴⁰Ar atom is small enough—more than 10 times smaller² than the inter-crystalline distances in sanidine³—that it can move freely between a rock suite and its surrounding environment. Clearly, the closed-system assumption (i.e., that the rock sample being tested has not interacted with its environment) cannot be reasonably presumed to hold for any significant period of time in the K-Ar system, much less for millions or billions of years.

Radioactive potassium (⁴⁰K) only constitutes 0.0117% of the potassium in nature. This fact, coupled with its extremely long half-life, makes it an experimental challenge to separate its decay product ⁴⁰Ar from primeval and cosmogenically produced ⁴⁰Ar in any rock sample; i.e., extremely small amounts of ⁴⁰Ar are generated by decay of ⁴⁰K. Thus, it becomes impossible to definitively determine which ⁴⁰Ar is the result of ⁴⁰K decay and which is the result of another process. This can have a profound effect on obtaining a reliable date as the initial presence or addition of even small amounts of ⁴⁰Ar to a rock suite or any samples contained within the rock would cause the sample to appear older than it really is.

Dating using the potassium-argon (K-Ar) clock employs three different methods. As Paul has exhorted us to test all things (1 Thessalonians 5:21), let’s carefully look at these three methods:

1. The straightforward potassium-argon (K-Ar) solution method
2. The isochron method
3. The argon-argon (Ar-Ar) method

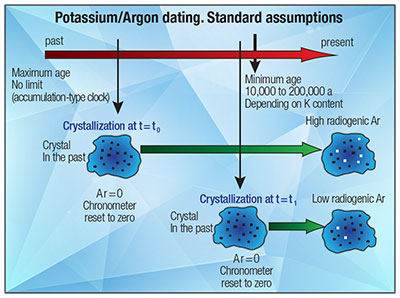
In the straightforward solution method, the concentration of ⁴⁰Ar is assumed to have been zero when the rock suite specimen crystallized, and therefore any ⁴⁰Ar that is present is considered to be the result of ⁴⁰K decay.

From recent experimental evidence,⁷ we know that assumption 7 (Sidebar A) does not hold. Assumptions 2, 3, 4, and 5 are all closed-system assumptions that are not realistic, especially in secular deep-time frames. Assumption 8 is strongly dependent on the methodology used and the personnel making the measurements. ³⁹K, the most abundant isotope of potassium (93.3%), is easily converted to ⁴⁰K by absorption of prompt and thermal neutrons,⁸ and therefore assumption 6 does not rigorously hold. Finally, to assume that ⁴⁰Ar cannot move at least somewhat freely through a rock matrix is unreasonable—so scratch assumption 1.

Of the eight assumptions, none can be considered to rigorously hold in all situations. Therefore, dating by this method is at best a hypothesis concerning the age of any rock suite or mineral; it is certainly not a scientific fact!

In the straightforward model for K-Ar dating, it was assumed that no primeval, outgassed, absorbed, or cosmogenic (i.e., caused by cosmic rays) ⁴⁰Ar existed in the rock matrix being analyzed. As pointed out in last month’s Acts & Facts article,⁹ this is a shaky assumption. So the K-Ar straightforward method becomes the K-Ar isochron method by adding the original concentration of argon 40 (⁴⁰Ar)_o to the right side of the equation and dividing both sides of the equation by non-radiogenic ³⁶Ar (an isotope not produced by radioactive decay that is used as an index isotope).

Assumption 9 (Sidebar B) is simply a contradiction for any whole-rock sample and only workable for a collection of different mineral samples contained in the same rock suite. The family of potassium feldspars have a wide range of blocking temperatures (~900°C to 135°C), and therefore assumption 10 is not generally applicable—meaning one cannot definitively differentiate between a true isochron and a mixing line (an imperfect mixing of two or more rock types). Methods of correcting for atmospheric absorption of argon are still quite hypothetical,¹⁰ making assumption 11 questionable. Assumptions that are integral to both these K-Ar dating methods make the dates obtained with them hypothetical estimates at best; but again, they are certainly not scientific fact.

The third method for dating rock suites using the K-Ar decay chain as a clock is commonly referred to as the argon-argon (Ar-Ar) method. This method avoids the homogeneity problem for whole-rock samples by only measuring isotope ratios of Ar, and it avoids the need for an index isotope such as ³⁶Ar. It also avoids the problem of accurately measuring the absolute concentrations of potassium and argon (assumption 8), so it is most often used to date very small or very rare samples such as meteorites or lunar rocks and minerals.

Now, in order to calculate the approximate age from the ⁴⁰Ar to ³⁹Ar ratio, one needs to evaluate J.¹¹ In order to directly calculate J, we must measure the ³⁹K to ⁴⁰K ratio and irradiation time accurately, and we must know the energy spectrum for the neutron flux (the number of neutrons per square centimeter per second in a given object) and the energy dependence of the (n,p) reaction cross-section (the probability that a neutron incident on a ³⁹K nucleus will produce a proton and an ³⁹Ar nucleus) over that entire energy spectrum. Unfortunately, the (n,p) cross-sections over the entire reactor neutron energy range are not well known and neither is the energy spectrum. So, a flux monitor of known age is irradiated with the rock sample, and the measured ⁴⁰Ar to ³⁹Ar ratio for that monitor, or standard, provides the J for that particular irradiation. Two questions immediately arise: How do we know the age of the flux monitor, and how good is the assumption that ⁴⁰K, ⁴⁰Ar, and ³⁹Ar are unaffected by the irradiation process?

When a rock sample is irradiated with a broad spectrum of neutrons, such as those produced by a nuclear reactor, many competing reactions occur simultaneously. Competing reactions for various Ar isotopes can invalidate the dating process. They are listed in Faure’s Principles of Isotope Geology.¹² This means that a series of corrections must be made¹³ that are especially serious for “young samples” less than one million years old (< 106 years) and those having significant concentrations of Ca (i.e.,   K  < 1.0).

In addition to the eight assumptions that go into the straightforward model, it must also be assumed that all measurable ³⁶Ar originates from atmospheric diffusion into the rock matrix, all measurable ³⁹Ar is produced by the (n,p) reaction on ³⁹K, and the isotope production factor, J, can be accurately correlated with the decay of ⁴⁰K into ⁴⁰Ar. For any mineral with a substantial chlorine (Cl) content, the assumption concerning ³⁶Ar becomes problematic since the neutron capture cross-section for ³⁵Cl (which indirectly produces ³⁶Ar through the beta decay of ³⁶Cl) is approximately 44 barns (10^-24 cm²), a very large production cross-section for the most abundant form of chlorine.

The second assumption—i.e., all measurable ³⁹Ar is produced by the (n,p) reaction at nuclear reactor energies—appears to be a reasonable assumption provided spallation¹⁴ cross-sections on transition metals such as scandium, calcium, titanium, cobalt, nickel, and iron are comparatively small. The only way to correlate the decay of ⁴⁰K into ⁴⁰Ar to the reactor production of ³⁹Ar is through the nuclear reaction constant J, but J must be determined using a standard of known age—this is clearly a circular methodology! Besides all the dubious assumptions that go into it, this method is deliberately biased by the standard used to determine J. This appears to be academic propaganda rather than good science.

Other than the unreasonable assumptions that form an integral part of all three K-Ar dating methods, there are many examples listed by Andrew Snelling in Radioisotopes and the Age of the Earth in which the methods give erroneous K-Ar dates.¹⁵ Thus, the K-Ar model does not meet even the basic criteria of a hypothesis in the scientific method.

Researchers who use results from these dating methods to conclude that rock sample dates are evidence of a millions or billions-year-old Earth are simply not using a legitimate scientific method. Dating methods that use better assumptions which can reliably reproduce known ages of rocks are needed. The potassium-argon dating method—once heralded as a solid scientific method—has proven to be unreliable.

Click here to read “Clocks in Rocks? Radioactive Dating, Part 1.”

Click here to read “The Iconic Isochron: Radioactive Dating, Part 2.”

Click here to read “Alkali Metal Dating, Rb-Sr Dating Model: Radioactive Dating, Part 4.”

References

1. MeV is an abbreviation for the energy unit of one million electron volts. One eV is defined as the amount of energy gained (or lost) by the charge of a single electron moved across an electrical potential difference of one volt. One MeV is 106 eV.
2. Hurlbut, C. S., et. al. 1977. Manual of Mineralogy, 19th ed. New York: John Wiley & Sons, 428.
3. Sanidine is potassium feldspar mineral, KAlSi3O8, which is considered the best specimen for dating using the K-Ar methodology.
4. Faure, G. 1986. Principles of Isotope Geology, 2nd ed. New York: John Wiley & Sons, 67.
5. Blocking temperature, or more generally closure temperature, is defined as the temperature at which the loss of ⁴⁰Ar by diffusion out of a given mineral or rock suite is negligible compared with its rate of accumulation.
6. Fractionation is the separation of isotopes through chemical and physical processes and occurs frequently during the cooling of igneous rocks as they come into the crust and solidify.
7. Cupps, V. 2014. Clocks in Rocks? Radioactive Dating, Part 1. Acts & Facts. 43 (10): 8-11.
8. Cross-sections for the reaction ³⁹K(n, γ)⁴⁰K range from approximately two barns (10^-24 cm²) for three MeV neutrons to 1,000 barns for one eV neutrons. These are very large cross-sections for nuclear reactions.
9. Cupps, V. 2014. The Iconic Isochron: Radioactive Dating, Part 2. Acts & Facts. 43 (11): 10-13.
10. Faure, Principles of Isotope Geology, 74.
11. J is the isotope production factor. In order to evaluate the amount of ³⁹Ar generated during the irradiation of ³⁹K, the amount of ³⁹K must be known as well as the time over which the irradiation occurs, the number (flux) of neutrons of a given energy which strike the sample during the irradiation, and finally the cross section (or probability of the reaction occurring) at the given energy. Summing (integrating) the product of these factors over the entire energy spectrum of the neutrons generated by a specific nuclear reactor will then yield the amount of ³⁹Ar formed by the irradiation.
12. Faure, Principles of Isotope Geology, 95.
13. Brereton, N. R. 1970. Corrections for Interfering Isotopes in the ⁴⁰Ar/³⁹Ar Dating Method. Earth and Planetary Science Letters. 8 (6): 427-433.
14. Spallation is the process by which a nuclear projectile, such as a proton or neutron, breaks a target nucleus into two or more component parts.
15. Snelling, A. A. 2000. Geochemical Processes in the Mantle and Crust. In Radioisotopes and the Age of the Earth: A Young-Earth Creationist Research Initiative. El Cajon, CA: Institute for Creation Research and St. Joseph, MO: Creation Research Society, 128.

* Dr. Cupps is Research Associate at the Institute for Creation Research and received his Ph.D. in nuclear physics from Indiana University-Bloomington.