We don’t know what we are talking about. Many of us believed that string theory was a very dramatic break with our previous notions of quantum theory. But now we learn that string theory, well, is not that much of a break. The state of physics today is like it was when we were mystified by radioactivity. They were missing something absolutely fundamental. We are missing perhaps something as profound as they were back then.

— David Gross at 23rd Solvay Conference in December 2005

Radioactive dating is a key concept in determining the age of the earth. Many secular scientists use it to dismantle the faith of Christians and cause them to accept uniformitarian assumptions that, in addition to being scientifically erroneous, demand a figurative and distorted interpretation of Genesis. Being knowledgeable about such a widespread dating method is essential for Christians to address opposing arguments and critics. Is radioactive dating valid?

Natural radioactivity was discovered in 1896 by the French physicist Henri Becquerel. A decade later, American chemist Bertram Boltwood suggested that lead was a disintegration product of uranium and could be used as an internal clock for dating rocks. By the mid-1940s, Willard Libby realized that the decay of ¹⁴C might provide a method of dating organic matter. He proposed that the carbon in living matter might include ¹⁴C as well as non-radioactive carbon. For ¹⁴C research—his life’s work—Libby was awarded the Nobel Prize in Chemistry in 1960, and the age of radioactive dating was born.

Before we delve into radioactive decay and its use in dating rocks, let’s review some essential nuclear physics concepts.

Each atom is made up of protons and neutrons concentrated in the atom’s center—its nucleus—around which electrons orbit. The protons and neutrons form the nucleus of an atom with approximate diameters ranging from 1.75 fm for the hydrogen atom to 15 fm for the uranium atom.¹ This nucleus contains approximately 99.94% of the atom’s total mass. The smallest electron orbitals range from approximately 1.06 Å for the hydrogen atom to 3.5 Å for the uranium atom.² Thus, the closest electrons orbit approximately 100,000 times farther from the center of the nucleus than the outermost nucleons.³ This means that the atom is mostly empty space as Ernest Rutherford aptly demonstrated with his alpha particle-gold foil scattering experiment in 1911.⁴

The chemical properties of each element are defined by the number of protons it contains in its nucleus and, consequently, the number of corresponding electrons that orbit it. However, elements beyond hydrogen’s single proton have varying numbers of neutrons that do not necessarily equal the amount of protons in the nucleus. This feature of nuclear construction produces elemental families, groups of elements with the same number of protons but differing numbers of neutrons. Because these families have the same number of protons in the nucleus, they also have the same number of electrons orbiting the nucleus and thus exhibit the same chemical behavior. It is the differing number of neutrons that give rise to stable and unstable isotopes (radioisotopes) within a given elemental family. As it turns out, nearly every element from Hydrogen (Z=1) to Bismuth (Z=83) has at least one stable isotope, with Technetium (Z=43) and Promethium (Z=61) as the exceptions. All elements above Bismuth in the Periodic Table are unstable, i.e., they are in a constant state of releasing energy, or decaying.

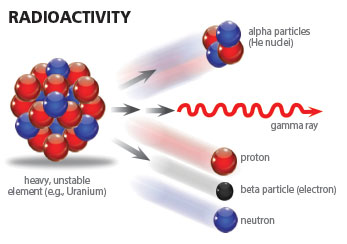
Alpha decay generally occurs only in the heavier radioactive nuclides, i.e., radionuclides, (A≥146) and can be thought of as an attempt to stabilize the nuclear charge to mass ratio.^5,6 For alpha emission, the decay energy is manifest as the kinetic energy of the ejected alpha particle (α). It is this type of radioactive decay which produces radiohalos in rock-contained minerals.⁷ Each nucleus that alpha decays produces a unique set of alpha-particle energies. As these alpha particles travel through a mineral matrix, they deposit their energy in the mineral itself. This energy damages the crystalline structure of the mineral and leaves in its wake a signature in the form of a series of discolored concentric rings—radiohalos—characteris
tic of the radionuclide that produced the alpha particles. Interestingly, it is in these radiohalos we find the best indirect observational evidence, measured at today’s rates of decay, supporting millions of years of radioisotope decay. These radiohalos originate from tiny point-like inclusions of ²³⁸U or some other naturally occurring radioisotope within the crystal.

Unfortunately for the secularist, there are radiohalos formed from what appears to be primordial Po (polonium), rather than Po in the form of daughter isotopes from U decay. Due to the extremely short half-lives of the Po isotopes, this would present a serious problem for those wanting to date the rocks at millions or billions of years old. Diffusion rates of the ⁴He (helium)—produced by the associated decay chains out of the crystals and the buildup of ⁴He in the atmosphere—suggest that only thousands of years of decay have occurred.⁸ Thus, the observed evidence in rocks extracted from the earth’s crust present several conundrums—problems that center on assumptions made in using radioisotope decay within a rock sample as a clock to date the origins of that sample. These issues will be detailed in subsequent articles.

In the processes of beta and positron decay, the energy is shared between the emitted beta or positron particles and an antineutrino or neutrino respectively. This makes energy spectroscopy for these decays more challenging than for alpha or gamma decays. If the parent nucleus decays to an excited state of the daughter nucleus for any of the above decays, then gamma rays can also accompany the emitted particles.

Less common modes of decay are direct emission of a neutron or proton, double-beta decay, and spontaneous fission. As with alpha decay, these modes are generally observed in the heavier radionuclides with a few exceptions such as ⁵³Co (proton emission), ¹³Be, and ⁵He (neutron emission).

The process of radioactive decay can be envisioned as an hourglass implanted in a rock suite. The parent radioisotope would be approximately represented by the sand in the upper chamber and the daughter radioisotope (what an element slowly turns into through decaying) by the sand that accumulates in the lower chamber. The throughput rate, the rate at which the sand accumulates in the bottom chamber, is characteristic of a specific decay sequence and can be viewed as roughly analogous to the neck of the hourglass, which controls the rate at which the sand falls. (See Figure 1 below.)

Secularists believe that nuclear decay has been a part of the natural world since its formation some 13.8 billion years ago, and the nuclear decay rates for the various radioisotopes have been constant throughout that time. This perspective, generally termed the uniformitarian view of nature, constitutes a pillar of the secularist’s worldview and is fundamental in generating the concept of deep time in the origins discussion. The Bible defines this view well in 2 Peter 3:3-4:

…knowing this first: that scoffers will come in the last days, walking according to their own lusts, and saying, “Where is the promise of His coming? For since the fathers fell asleep, all things continue as they were from the beginning of creation.”  

Unfortunately for the secularist, there are serious problems with the uniformitarian view as it is applied to radioactive dating. Recent experimental evidences verify that the decay rates of radioisotopes can vary significantly from the currently accepted values—by as much as 10⁹ times faster (that’s 1 billion times faster) when exposed to certain environmental factors.^9,10,11 It is particularly interesting that the alpha-decay rates of ²²⁸Th are increased by as much as 10⁴ (10,000 times) under conditions which give rise to high pressure waves.¹⁰ These conditions could have easily existed during the Flood. One cannot help but wonder what this might say about nuclear decay processes inside stars or large exoplanets.

There are significant problems with the radioactive dating methodology currently employed by secularists. The closed-system assumption—so critical to all radioactive dating methods—strains credibility when applied over millions of years. Can any system remain unaffected by its environment over millions of years?

The Bible is clear that the earth is relatively young, little more than 6,000 years old. An excellent literary argument supporting that position is presented by Steven Boyd,¹² and indeed there have been many others throughout the centuries. When properly applied, science does not contradict this position. Passages such as Psalm 18:7-8, 11-16, Habakkuk 3:8-10, 15, and Deuteronomy 32:22 all seem to suggest that radioactive decay may not have been a part of God’s original creation. Perhaps radioactivity first appeared as a response to the curse of man’s sin, originally residing deep in the earth’s interior during the antediluvian period and being moved up into the earth’s crust through tectonic activity during the Flood.

In the refreshingly honest words of Dr. David Gross, perhaps we still don’t know nearly as much about radioactivity as we think we do.

Click here to read “The Iconic Isochron: Radioactive Dating, Part 2.”

References

1. A Fermi (fm) is a unit of measure equal to 10^-15 meters. It is usually used to express inter-nuclear distances.
2. An Angstrom (Å) is a unit of measure equal to 10^-10 meters. It is usually used to express inter-atomic distances.
3. Nucleon is a term used to collectively identify the two major constituents of the nucleus, i.e., the protons (Z) and neutrons (N). The number of nucleons in a given nucleus is designated by the letter A (= Z + N).
4. In 1911, Ernest Rutherford performed an experiment to test the Plum Pudding Model of the atom. He fired energetic α [He²⁺] particles at a sheet of gold foil and measured the deflection of the particles as they came out the other side. From this, he deduced that the atom was mostly empty space because very few α particles experienced any measureable deflection from their initial path.
5. A radionuclide is any nucleus of a given elemental family which is radioactively unstable.
6. The charge to mass ratio (^Q/_m) for any nucleus is the ratio of the number of protons (Z), which define the elemental family of that nucleus, to the number of protons plus the number of neutrons resident in that nucleus (A). Mathematically: ^Q/_m = ^Z/_A
7. Snelling, A. 2000. Radiohalos. In Radioisotopes and the Age of the Earth, Volume I, edited by L. Vardiman, A. Snelling, and E. Chaffin, Dallas, TX: Institute for Creation Research.
8. Humphreys, R. 2005. Young Helium Diffusion Age of Zircons Supports Accelerated Nuclear Decay. In Radioisotopes and the Age of the Earth, Volume II, edited by L. Vardiman, A. Snelling, and E. Chaffin. Dallas, TX: Institute for Creation Research.
9. Bosch, F. et al. 1996. Observation of Bound-State β − Decay of Fully Ionized ¹⁸⁷Re: ¹⁸⁷Re−¹⁸⁷Os Cosmochronometry. Physical Review Letters. 77 (26): 5190-5193.
10. Cardone, F. et al. 2009. Piezonuclear decay of thorium. Physics Letters A. 373 (3795): 1956-1958.
11. Jenkins, J. H., D. W. Mundy, and E. Fischbach. 2010. Analysis of environmental influences in nuclear half-life measurements exhibiting time-dependent decay rates. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 620 (2-3): 332-342.
12. Boyd, S. 2005. Statistical Determination of Genre in Biblical Hebrew: Evidence for an Historical Reading of Genesis 1:1-2:3. In Radioisotopes and the Age of the Earth, Volume II, edited by L. Vardiman, A. Snelling, and E. Chaffin. Dallas, TX: Institute for Creation Research.

* Dr. Cupps is Research Associate at the Institute for Creation Research and received his Ph.D. in nuclear physics from Indiana University-Bloomington.