…that we should no longer be children, tossed to and fro and carried about with every wind of doctrine, by the trickery of men, in the cunning craftiness of deceitful plotting. (Ephesians 4:14)
This final article of the series examines the common-lead method of radioactive dating, sometimes referred to as the Pb-Pb method. This method reaches the pinnacle of radioisotope dating methods in terms of complication and convolution. Since we do not want to be tossed to and fro by every teaching that cunning men put in front of us, let’s carefully investigate this method’s viability as a reliable clock for terrestrial and extraterrestrial rock formations.
Our investigation begins with the three “so called” isochron equations listed in a previous Acts & Facts article that are the foundation for the U-Pb and Th-Pb dating methods.1 Straightforward application of these equations generally yields discordant results; i.e., the dates obtained disagree by more than the stated measurement errors allow.2 In fact, Gunter Faure states that this must be taken as evidence that one or more of the dating method assumptions are not satisfied—essentially nullifying the method.3
In an attempt to solve this problem, the isochron equation for 235U is divided by the isochron equation for 238U to yield an isochron equation that only involves Pb isotope concentrations on one side of the equation:
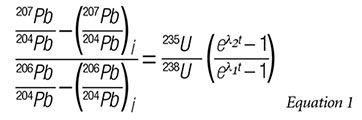
The result is a transcendental equation that cannot be solved for t (time). Now we must make some adjustments to the equation in order for it to be practically useful—adjustments that involve dubious assumptions.
First, we assume, as a corollary to the closed system assumption, that 206Pb and 207Pb concentrations only change via decay of 238U and 235U respectively.
Second, we assume that the present-day isotope ratio of 235U/238U is constant in time even though they have different decay constants.
Third, we assume that a clever application of l’Hôpital’s rule from elementary calculus will provide us with a reasonable primordial value for the radiogenic Pb ratio, i.e., (207Pb/206Pb),* that is good for all terrestrial and extraterrestrial rocks. We are then left with the following equation for dating rocks based solely on their radiogenic 207Pb and 206Pb concentrations:
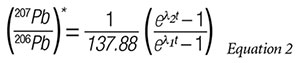
Numerical solution of this equation, by projecting it forward in time from the present measurements of 207Pb, 206Pb, and 235U/238U= 1/137.88, yields a fourth estimate of a rock’s age. However, a critical question arises: How do we know the initial concentrations of the radiogenic 207Pb and 206Pb concentrations in the rock we are dating?
At t=0, the equation for radiogenic Pb isotopes is indeterminate since it results in division by 0. Secular scientists get around this problem by a clever application of l’Hôpital’s rule to estimate that the original ratio is (207Pb/206Pb)* = 0.04604. They then measure the present radiogenic lead ratio in a rock sample and interpolate the age of the sample from a table of age versus the radiogenic lead ratio constructed from Equation 2. This estimate is generally discordant with the first three isochron estimates. However, Faure believes that this last estimate is most likely also discordant due to loss of radiogenic Pb by thermal metamorphism or various other transport mechanisms.4 He further concludes that if this is the case, then the (207Pb/206Pb)* date is the most reliable. If the loss of radiogenic Pb is possible, then shouldn’t the gain of radiogenic Pb also be possible? It would not take much Pb gain to significantly skew the age to a much younger value.
Secular scientists attempt to understand these discordances by constructing U-Pb Concordia diagrams, such as in Figure 1. They reason that if one plots the ratio of radiogenically generated Pb to its corresponding U isotope on a two-dimensional plot, then one obtains the ideal curve describing the evolution of radiogenic Pb in closed-rock formations. They further reason that the loss of radiogenic Pb out of the rock formation causes discordant lines that intersect the ideal curve at the time of original crystallization and the time elapsed since complete closure to migration of any form, assuming all assumptions are rigorously satisfied. In this way, the Pb-Pb method attempts to deal with any loss of radiogenic Pb during the life of the rock formation.
The time points on the graph indicate values for the t (time) inserted into the equations for (207Pb/235U)* and (206Pb/238U)*, i.e.:
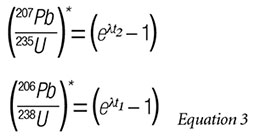
Note that one obtains two different closure times for the rock sample depending on which minerals are selected to define the concentration line underneath the Concordia arc. This is the basic Pb-Pb dating method for rock samples.
The ratios of U/Pb and Th/Pb must be quite large to maximize the sensitivity of these dating methods to radiogenically generated Pb. Thus, they can only be applied to certain minerals such as zircon and monazite crystals.5 In order for any of these methods to provide reasonable estimates of the age of a rock, all four basic assumptions made for radioisotope dating methods must be rigorously satisfied:
(1) The rock/mineral must have remained closed to U, Th, Pb, and all intermediate daughters throughout its history.
(2) The decay constants of U, Th, Pb, and all intermediate daughters must be accurately known and constant over the entire history of the rock.
(3) The primordial concentrations of all U, Th, and Pb isotopes used in estimating the age are accurately known.
(4) Enough time has elapsed for the formation of measurable amounts of radiogenic Pb.
For the Pb-Pb method, a further assumption is employed—that the isotopic composition of U has not been modified over the age of the rock. This is a demonstrably bad assumption, because we know from observation that 235U is significantly depleted with respect to 238U in the Precambrian deposits at Oklo, Gabon, Africa, due to naturally induced neutron fission within the deposits.6 Logic would also suggest that the isotopic composition of U would change over billions of years since 235U decays approximately seven times faster than 238U.
An even more mathematically complex model called the Holmes-Houtermans Model (hypothesis), using only Pb isotope concentrations, has been developed to date the age of the earth and extraterrestrial rocks.7 It makes five more assumptions, which are essentially corollaries to the closed system assumption, plus a sixth assumption unique to the Pb-Pb dating system. The sixth assumption assumes that at the time a mineral was formed in a rock, the Pb it contains was separated from the U and Th parents, and thus its isotope ratio has remained constant. How does one use radioisotope decay as a clock when it has been removed from the rock sample being dated? Secular scientists assume that the galena (lead sulfide) being dated is a certain age based on the traditional stratigraphic dating of the earth rock layers. The gold standard for dating has turned to lead (Pb)!
Examples abound of discordant and just plain wrong dates obtained with these gold-standard dating methods. Rock samples from New Zealand’s Mt. Ngauruhoe yielded a Pb-Pb isochron age of 3.908 ± 0.390 x 109 yrs. for samples known to be ≤ 60 yrs. old. Somerset Dam layered mafic intrusion rocks gave a Pb-Pb isochron age of 1.425 ±1.000 x 109 years for samples having a conventional age of 0.216 ± 0.004 x 109 years.8 Why would anyone accept them as scientific fact when they aren’t based on reasonable assumptions and don’t faithfully reproduce empirical data?
I hope you enjoyed this series. I presented these issues in detail because scientists and lay people alike deserve a thorough and comprehensive answer. I believe you can now see that all radioisotope dating methods are fraught with questionable assumptions and do not reproduce observable data as the scientific method requires. In conclusion, radioisotope dating presents no rational basis for believing that science has contradicted the Bible and its clear account of creation—on the contrary, the data point to a young earth and universe!
Click here to read the previous articles in this series.
References
- Cupps, V. R. 2015. Heavy Metal Clocks, U-Pb and Th-Pb Dating Models: Radioactive Dating, Part 7. Acts & Facts. 44 (5): 10-11.
- Faure, G. 1986. Principles of Isotope Geology, 2nd ed. New York: John Wiley & Sons, 291.
- Ibid, 290.
- Ibid, 291.
- Faure, G. and T. M. Mensing. 2005. Isotopes: Principles and Applications, 3rd ed. New York: John Wiley & Sons, 221.
- Faure, Principles of Isotope Geology, 288.
- Ibid, 256.
- Snelling, A. 2005. Isochron Discordances and the Role of Inheritance and Mixing of Radioisotopes in the Mantle and Crust. In Radioisotopes and the Age of the Earth: Results of a Young-Earth Creationist Research Initiative. Vardiman, L., A. A. Snelling, and E. F. Chaffin, eds. El Cajon, CA: Institute for Creation Research, and Chino Valley, AZ: Creation Research Society.
* Dr. Cupps is Research Associate at the Institute for Creation Research and received his Ph.D. in nuclear physics from Indiana University-Bloomington.













