Is Genesis 1:1-2:3 a historical narrative (with the plain sense of its words corresponding to reality and the sequence of events portrayed correlating with real time) or is it an extended poetic metaphor? Answering this vital question has been the focus of my RATE research, the results of which will appear as a chapter in the final RATE book.1 Below is just a sample of the exciting results of this study: paired-texts data, control charts, and logistic regression.
The priority of the text: a statistical approach
Although the Hebrew text's ordinary morphology, syntax, and vocabulary betray no indication that it should be read other than as a narrative, many who hold to an old earth model, read it as mere poetry. But is this approach defensible? I'm convinced the text will tell us whether the author wanted us to read it as poetry or prose: countable linguistic features—which allow statistical analysis—can inform us of what his original readers would have intuitively grasped.2 I chose to study the distribution of Biblical Hebrew finite verbs (verbs inflected for person, gender, and number), to find the answer.
A statistically valid, stratified random sample of 48 narrative and 49 poetry texts was generated from all the narrative and poetry texts and then subjected to statistical tests in order to answer two questions: (1) Is the finite verb distribution dependent on genre (poetry versus narrative)? and (2) If it is, can the distribution in a given text be used to determine its genre?3
Paired-texts data
The paired-texts data plot (figure 1) contrasts the distributions of finite verbs for narrative and poetic versions of the same event: the crossing of the Red Sea (Exodus 14, narrative; Exodus 15:1-19, poetry); Baraq and Deborah defeating the Canaanites (Judges 4, narrative; Judges 5, poetry). In addition, Genesis 1:1-2:3; Psalm 104 (a poetic account of creation); Genesis 6-9 (the Flood); and two historical psalms, 105 and 106, were plotted. Preterite verbs (green) clearly dominate in narrative.4 On the other hand, imperfects (red) and perfects (yellow) clearly dominate in poetry.
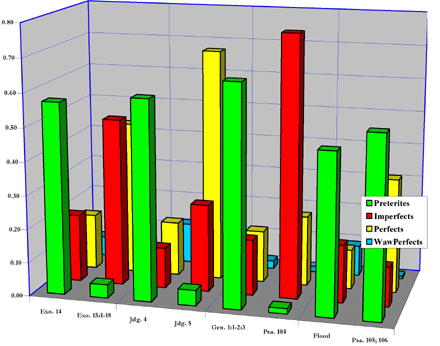 |
| Figure 1. 3-D plot of paired-texts data, showing contrasting finite verb distribution for narrative versus poetry texts portraying the same event. |
Relative Frequency
Ex. 14
Ex. 15:1-18
Jdgs. 4
Jdgs. 5
Gen. 1:1-2:3
Ps. 104
Flood
Ps. 105; 106
Control charts
In control charts, data points within three standard deviations of the mean have a 99.73 percent probability of belonging to that population; whereas points outside these control limits do not belong. The charts showed that the mean of the ratios of preterites to finite verbs for narrative differs from poetry. Finite verb distribution, therefore, is dependent on genre. Moreover, since Genesis 1:1-2:3 was far outside the upper control limits for poetic texts, it is not part of that population.
Logistic regression: model evaluation
Logistic regression is ideal for our data, because a text is either a narrative or poetry, with assigned probabilities (P) of 1 and 0, respectively.5 We determined the coefficients of the equation for the curve that fit this non-linear data by maximizing the logarithm of the odds (P/(1-P)) for the ratios of preterites to finite verbs for the 97 texts analyzed.6
To determine our model's goodness of fit, we calculated the "model chi-squared" statistic to test the null hypothesis that our model did no better than the model with zero coefficients.7 Our model rejected this null hypothesis at a highly statistically significant level.8
We also determined R2L , a measure of the substantive significance of the model, that is, how much does the model reduce the variation from the zero coefficients model. R2L ranges from 0 (poor model) to 1 (perfect model).9 For our model R2L was .85 for the unweighted, .88 for the weighted—highly effective in reducing the variation.
Logistic regression: classification accuracy
A perfect classification model would classify all passages into their actual genre. Our model misclassified only 2 out of 97 passages.
Classification accuracy is indicated by proportional change in error (tP),10 which measures how much the model reduces error: tP = ((errors without the model) - (errors with the model))/(errors without the model).
The expected number of errors without the model for a classification model is
2nY=0nY=1/N , where nY=0 is the number of poetic texts examined, nY=1 is the number of narrative texts examined, and N is the total number of texts examined.
If tP equals 1, the model is a perfect classifier; if tP is negative, the model did worse than random classification. For our model tP was 0.96—highly substantively significant.11
The binomial statistic was used to test the null hypothesis that the proportion incorrectly classified by the model is no lower than that of random classification. Our model also rejected this null hypothesis at a highly statistically significant level.12 Our model is a superb classifier.
Logistic regression: identifying the genre of texts
Rejection of the null hypotheses means that the logistic curve for our model (figure 2) identifies genre extremely accurately. In figure 2 red squares represent the poetic texts, green diamonds the narrative texts, and a pink triangle Genesis 1:1-2:3. Points on the curve are the probability that a text is a narrative for a given ratio of preterites to finite verbs. Using this curve the probability that Genesis 1:1-2:3 (X1 = 0.655) is a narrative is 0.999972604.
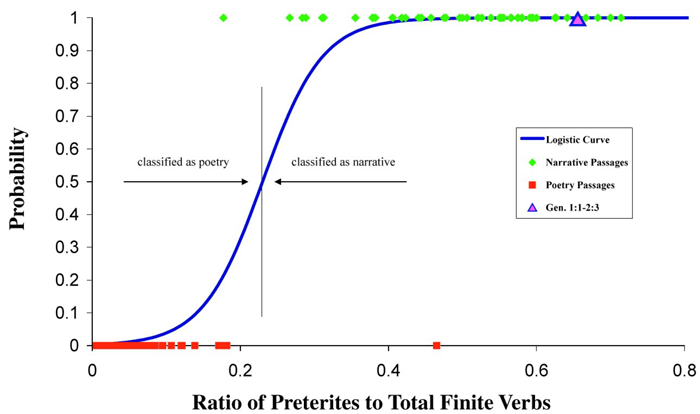 |
| Figure 2. Logistic regression curve showing the probability a passage is a narrative based on its ratio of preterites to finite verbs. |
Conclusion
The distribution of preterites to finite verbs in Hebrew narrative differs distinctly from that in Hebrew poetry. Moreover, a logistic regression model fitted to the ratio of preterites to finite verbs categorizes texts as narrative or poetry to an extraordinary level of accuracy. With its probability of virtually 1, Genesis 1:1-2:3, therefore, is a narrative, not poetry.
Three major implications from this study are (1) it is not statistically defensible to read Genesis 1:1-2:3 as poetry; (2) since Genesis 1:1-2:3 is a narrative, it should be read as other Hebrew narratives are intended to be read as a concise report of actual events, couched to convey an unmistakable theological message;13 and
(3) when this text is read as a narrative, there is only one tenable view of its plain sense: God created everything in six literal days.
Endnotes and References
- RATE stands for "Radioisotopes and the Age of The Earth," a research initiative launched in 1997 jointly by the Institute for Creation Research, the Creation Research Society, and Answers in Genesis.
-
For how an author's relationship with his original readers should affect the reading of texts, see Nicolai Winther-Nielsen, "Fact, Fiction and Language
Use: Can Modern Pragmatics Improve on Halpern's Case for History in Judges?" in V. Phillips Long et al, eds. Windows into Old Testament History: Evidence, Argument, and the Crisis of "Biblical Israel" (Grand Rapids: Wm. B. Eerdmans Publishing Co., 2002), pp. 44-81. - Dr. Roger Longbotham, Senior Statistician for Amazon.com, was the statistical consultant for this study.
- Preterites form the "backbone" of Hebrew narrative. See among others Jerome Walsh, Style and Structure in Biblical Hebrew Narrative (Collegeville, Minnesota: The Liturgical Press, 1996), pp. 155-172.
- Scott Menard, Applied Logistic Regression, 2nd Edition (Thousand Oaks, California: Sage Publications, 2002), pp. 67-91 and Fred Pampel, Logistic Regression: A Primer (Thousand Oaks, California: Sage Publications, 2000), pp. 1-18.
- The model representing X1 (preterites/finite verbs) is -5.39 + 22.44 X1 for unweighted data and -5.69 + 24.73 X1 for weighted data.
- Menard, pp. 17-22.
- For a two tailed test, p < .000001.
- Menard, p. 24.
- Ibid., pp. 28-40.
- For our data the expected errors without the model is 2(48)(49)/97, which equals 48.49. So, tP = (48.49 - 2)/48.49 = .96.
- The binomial statistic is computed as follows: d = (Pe - pe) / Ö Pe (1 - Pe)/N, where Pe is (errors without the model)/N and pe is (errors with the model)/N). For our model d was 9.44167264. So, p < 1.0 x 10-14.
- Meir Sternberg, The Poetics of Biblical Narrative: Ideological Literature and the Drama of Reading (Bloomington: Indiana University Press, 1987), p. 31.
* Steven W. Boyd, Ph.D. in Hebraic and Cognate Studies, is an Associate Professor of Bible at The Master’s College in Santa Clarita, California.