Did you know that more than one infinity exists—and some infinities are larger than other infinities? But if something is infinite, then how can something else be more infinite? These concepts are difficult for our finite mind to comprehend, but what’s fascinating about infinity is that it reflects the nature of God.

The Strangeness of Infinity

Infinity is the concept of an unlimited quantity. Something is infinite if it goes on forever, having no end. We tend to think of infinity as a really big number—but it is much more than that. A number like one million is big, but it is not infinite. As tedious as it would be, we can at least imagine counting from one to one million, and then we would be done. That set of numbers has an end. But infinity does not.

For this reason, infinity has some strange and counterintuitive properties that finite numbers lack.¹ For example, imagine that you had one million pennies. Suppose that you removed one penny every second and gave it to someone else. Over time, your pile of pennies would shrink. After 11 days, 13 hours, 47 minutes, you would have no pennies left.

Now suppose that you had an infinite supply of pennies and gave one penny away every second. Not only could you continue to do this forever without running out of pennies, but your pile would be no smaller than when you started. This is one of the weird things about infinity—you can subtract any finite number from it and yet it remains the same.²

By the same logic, you can add to infinity without changing it. Infinity plus one is exactly the same as infinity. Likewise, infinity plus one million is no larger than infinity. Even when we multiply infinity by a finite number, it remains unchanged. Thus, twice infinity is no larger than infinity. And yet, we can also prove that some infinities are genuinely larger than other infinities!

Comparing Sets

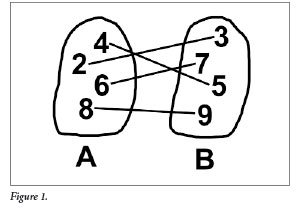To start, let us consider how we would compare sizes of sets of finite numbers. Consider the set of numbers 2, 4, 6, 8. We will call this set A. And suppose set B contains the numbers 3, 5, 7, 9 (Figure 1). In this case, we can say that set A and set B have the same size because we can count them both and they each contain exactly four elements. But we could also prove that they contain the same number of elements by showing that there is a one-to-one correspondence with each element in set A to exactly one element in set B. In other words, we can link the number 2 in set A with the number 3 in set B. Likewise, we link 4 to 5, 6 to 7, and 8 to 9. For each element of A there is exactly one element in B, and vice versa. Therefore, these two sets are the same size. We can apply this same reasoning to infinite sets as follows.

We define P as the set of all positive integers (1, 2, 3, 4, 5…). We then define set N as the set of all non-negative integers (0, 1, 2, 3, 4…). This is identical to set P, except set N also includes the number zero. Clearly, set N contains every number that set P contains and one more—the number zero. So, you might at first think that set N is larger than set P. But a moment’s thought shows that we can link every element in set N to an element in set P by adding 1. So we link 0 in N to 1 in P, we link 1 in N to 2 in P, and so on. For each element in N there is exactly one element in P, and vice versa. Thus, P and N are exactly the same size. Remarkably, infinity plus one is still infinity.³

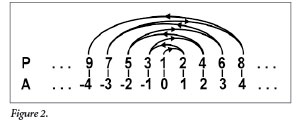Now, let’s consider a very counterintuitive example. Suppose we compare the set of positive integers P (1, 2, 3, 4, 5…) to the set of all integers A (…-4, -3, -2, -1, 0, 1, 2, 3, 4…) (Figure 2). The former is infinite in only the positive direction, whereas the latter is infinite in both directions. So, set A contains all of set P as well as an infinite set of all negative integers. So, you might think that set A must be larger than set P. But it is not. We can link every element of set P with an element of set A as follows.

We start counting with 1 in set P and match it to 0 in set A. Then we move to the next number to the right in A, then the next number to the left, then right, then left, and so on. So, the numbers in P (1, 2, 3, 4, 5…) will link to the numbers in A (0, 1, -1, 2, -2…). Clearly, for every integer there is exactly one corresponding positive integer. Thus, set A and set P are the same size! Even though set A contains all of set P as well as an infinite number of elements that are not in set N, nonetheless set A is the same size as set P. Apparently, infinity plus infinity is no larger than the original infinity.

Hilbert’s Hotel

German mathematician David Hilbert illustrated the strange-but-true properties of infinite sets in a thought experiment we now call Hilbert’s Hotel. He imagined a grand hotel with an infinite number of rooms (each labeled by a positive integer: 1, 2, 3, 4…) that could accommodate an infinite number of guests. Now, suppose that the hotel is full; every room is occupied. Then, one additional person comes to the front desk and asks for a room. You might suppose that the hotel manager would have to decline since every room is already booked. But in fact, the manager is able to accommodate the additional guest.

The hotel manager has each person in his hotel move into the room with the next number. That is, the person staying in the first room moves into the second. The person in the second room moves into the third, and so on. Since there is no “last room” in an infinite hotel, every person is able to move one number up, which leaves the first room empty. The hotel manager then puts the additional guest in the first room.

Suppose again that Hilbert’s grand hotel is full, with an infinite number of guests occupying an infinite number of rooms. This time, an infinite number of people show up at the front desk asking for a room. Since the hotel is already full, surely it cannot accommodate an infinite number of additional guests, can it? Once again, the manager finds a solution by reshuffling his current patrons. He asks each guest to move from room N to room 2N. That is, the person staying in room 1 goes to room 2, room 2 goes to room 4, room 3 goes to room 6, and so on. Since for every number N, there is a corresponding number 2N, every person is able to find a new room.

But a moment’s reflection shows that only the even-numbered rooms are now occupied (2, 4, 6, 8…). The odd-numbered rooms are empty, and there are an infinite number of odd-numbered rooms (1, 3, 5, 7…). So, the manager is able to accommodate each newcomer by assigning them to the odd-numbered rooms. Hilbert’s Hotel can accommodate even stranger scenarios. Infinity is a baffling concept.

Rational Numbers

Mathematicians refer to rational numbers as any number that can be expressed as a ratio of two integers, as with a fraction A/B. Examples include: 1/2, 3/4, 5/10, 178,672/234,297. Integers are also rational numbers because they can be expressed as a fraction over 1. That is 3 = 3/1. There are an infinite number of rational numbers. Amazingly, the number of rational numbers is equal to the number of positive integers.

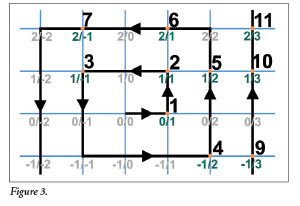This seems peculiar because not only does the set of rational numbers include all the positive integers, but there are an infinite number of rational numbers between any two positive integers. For example, between 1 and 2 we find fractions like 3/2, 4/3, 5/4, 6/5, 16,532/16,325…. Yet we can prove that these two infinite sets are the same size by plotting them on a plane as follows (Figure 3).

Let X and Y be integers that are the coordinates of a point on a plane. Y represents the numerator of a rational number and X the denominator. Thus, every possible fraction exists as a point somewhere on this grid. Starting at the origin, we trace a spiral-like pattern for every point at X and Y, and count one positive integer each time we land on a unique fraction. (But we don’t count duplicates such as 2/4, which equals 1/2, nor count division by zero—e.g., 0/0 or 1/0). Eventually, every X and Y combination will intersect the spiral and be assigned a positive integer. Thus, for every fraction (shown in green), there is a positive integer (shown in black). They are the same infinity.⁴

Uncountable Infinities

Paradoxically, all the infinite sets we have explored so far are the same size because each element in one matches an element in every other. Are any infinities genuinely larger than, say, the number of rational numbers? Amazingly, yes! All the aforementioned sets are countably infinite. This means if you systematically counted the elements of the set in the right order for all eternity, you will eventually hit them all. Countable infinity is the “smallest” infinity and is designated by the Hebrew letter aleph with a subscripted zero: ℵ₀.

But there are also uncountable infinities. For these, it is not possible to assign one positive integer to each member of the set, and you could never count them all even if you had unlimited time. In other words, there are not enough positive integers to assign one each to an uncountable infinity. The set of all real numbers is uncountably infinite. Real numbers include all rational numbers and all irrational numbers like pi or the square root of two. (Irrational numbers are those whose decimal expression goes on forever without repeating and cannot be expressed as a ratio of two integers.) Mathematician Georg Cantor showed that the set of real numbers is uncountable and thus a larger infinity than the rational numbers. Cantor was a Christian and was motivated to study infinity because it reflects the nature of God. Many mathematicians suspect that the set of real numbers is the second-smallest infinity⁵ —aleph one: ℵ₁. Of course, there are larger infinities: ℵ₂, ℵ₃, ℵ₄….

Infinity is one aspect of God’s nature. He is limitless in power, knowledge, and majesty. We are finite and cannot fully comprehend the concept of infinity. Yet, God made human beings in His own image, and so we have a sense of the infinite without fully understanding it. Those who have repented of sin and trusted in Christ for salvation will experience infinite time in God’s loving presence—eternity (John 3:16). Perhaps our fascination with the infinite is because God has set eternity in our hearts (Ecclesiastes 3:11).

References

1. The non-commutative nature of addition and multiplication of infinite quantities is one such example. For finite numbers, addition and multiplication are commutative—meaning the order doesn’t matter. For example, 2 + 3 = 3 + 2, and 12 × 3 = 3 × 12. But for infinite series, the order matters. An infinite series like A + B + C + D +… does not necessarily equal A + D + C + B +….
2. To be mathematically precise, the cardinality of an infinite set is unchanged by the subtraction or addition of any finite number of elements. This is not the case for finite sets. Cardinality is the mathematical term for the size of a set: the number of elements it contains.
3. The cardinality is unchanged.
4. The set of rational numbers has the same cardinality as the set of positive integers. However, the set of real numbers has a larger cardinality than the set of rational numbers.
5. The conjecture that the set of real numbers is the second-smallest infinity is called the continuum hypothesis.

* Dr. Lisle is Director of Physical Sciences at the Institute for Creation Research and earned his Ph.D. in astrophysics from the University of Colorado.